Answer:
a) 2001: P = 2457.106 thousand people
2006: P = 2398.813 thousand people
2011: P = 2327.899 thousand people
2015: P = 2260.998 thousand people
2020: P = 2163.573 thousand people
b) 2018
c) 2018
Explanation:
Given function:
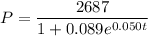
where:
- P = population (in thousands)
- t = number of years after the year 2000
Part (a)
In 2001, t = 1:

In 2006, t = 6:

In 2011, t = 11:

In 2015, t = 15:

In 2020, t = 20:

Part (b)
See attached for the graph of the function.
2.2 million = 2,200,000 = 2200 thousand
Therefore, draw a line at y = 2200.
The point of intersection between P(t) and y = 2200 is (18.223, 2200).
Therefore, the population will reach 2.2 million during 2018.
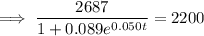
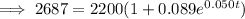
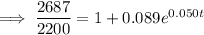
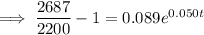
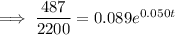
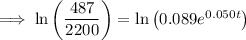
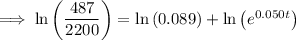
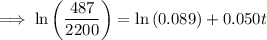
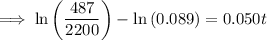
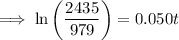
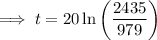
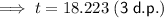
The population will reach 2.2 million in 2018.