Question

√4(x-5)^2=40 HELPPPPPPPPPPPPPP

Answer 1

x = 15

Explanation:

`(√(4(x -5)) ^(2)` = 40 If you square the square root of something, it would end up being itself.

4(x - 5) = 40

4x - 20 = 40 Add 20 to both sides

4x = 60 Divide both side by 4

x = 15

Answer 2

`√(4)(x-5)^2=40 \implies x=5 +2 √(5), \quad x=5-2 √(5)`

`√(4(x-5)^2)=40 \implies x=-15, \quad x=25`

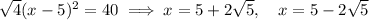
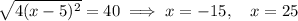
Explanation:

Given equation:

`√(4)(x-5)^2=40`

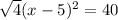
Simplify √4 = 2 :

`\implies 2(x-5)^2=40`

Divide both sides by 2:

`\implies (x-5)^2=20`

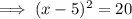
Square root both sides:

`\implies x-5=\pm √(20)`

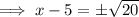
Simplify the right side of the equation:

`\implies x-5=\pm √(4 \cdot 5)`

`\implies x-5=\pm √(4) √(5)`

`\implies x-5=\pm 2 √(5)`

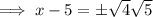
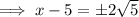
Add 5 to both sides:

`\implies x=5 \pm 2 √(5)`

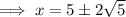
Therefore, the solutions are:

• 
  `x=5 +2 √(5)`
• 
  `x=5 -2 √(5)`

---------------------------------------------------------------------------------------

Given equation:

`√(4(x-5)^2)=40`

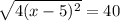
Square both sides:

`\implies 4(x-5)^2=1600`

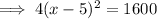
Divide both sides by 4:

`\implies (x-5)^2=400`

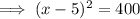
Square root both sides:

`\implies x-5=\pm √(400)`

`\implies x-5=\pm 20`

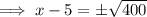
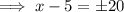
Add 5 to both sides:

`\implies x=5-20=-15`

`\implies x=5+20=25`

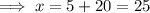
Therefore, the solutions are:

• 
  `x = -15`
• 
  `x = 25`