Answer:
t = 12 years
Explanation:
Given equation:
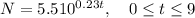
where:
- N = number of beavers
- t = time (in years)
To approximate how many years it will take for the beaver population, N, to reach 92, substitute N = 92 into the given equation and solve for t:

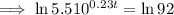
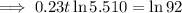
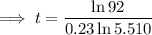
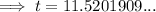
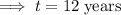
Therefore, it took 12 years (to the nearest year) for the beaver population to reach 92.