Question

Find the number of line segments with one endpoint A(20,24) and another endpoint on x -axis with integer coordinates, which have a common point with the line segment PQ, where P(0,4), Q(40,4)

Answer 1

49

Explanation:

To find the smallest and largest possible x-values of the endpoint on the x-axis, determine the equations of the lines that pass through point A and the endpoints of line segment PQ, then substitute y = 0 into each equation and solve for x.

Equation of line AP

Find the slope of the line that passes through point A and point P:

`\textsf{slope}\:(m)=(y_A-y_P)/(x_A-x_P)=(24-4)/(20-0)=(20)/(20)=1`

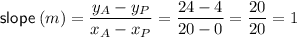
Substitute the found slope and one of the points into the slope-point formula to create an equation for line AP:

`\implies y-y_A=m(x-x_A)`

`\implies y-24=1(x-20)`

`\implies y-24=x-20`

`\implies y=x+4`

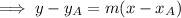
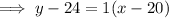
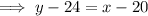
To find the point at which the line intersects the x-axis, substitute y = 0 into the found equation:

`\implies 0=x+4`

`\implies x=-4`

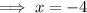
Equation of line AQ

Find the slope of the line that passes through point A and point Q:

`\textsf{slope}\:(m)=(y_A-y_Q)/(x_A-x_Q)=(24-4)/(20-40)=(20)/(-20)=-1`

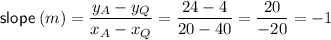
Substitute the found slope and one of the points into the slope-point formula to create an equation for line AQ:

`\implies y-y_A=m(x-x_A)`

`\implies y-24=-1(x-20)`

`\implies y-24=-x+20`

`\implies y=-x+44`

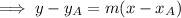
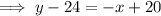
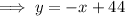
To find the point at which the line intersects the x-axis, substitute y = 0 into the found equation:

`\implies 0=-x+44`

`\implies x=44`

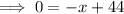
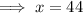
Therefore, the set of x-values for the other endpoint is -4 ≤ x ≤ 44.

An integer is a whole number that can be positive, negative, or zero.

As the x-value of the endpoint is an integer, it can take the value of all integers in the set [-4, 44].

Therefore, there are 49 line segments with one endpoint A (20, 24) and another endpoint on the x-axis which have a common point with the line segment PQ.