Question

a farmer has some chickens. he finds that together they have 70 heads and 200 legs. how many pigs and how many chickens does he have?

Answer 1

The farmer has 30 pigs and 40 chickens.

Explanation:

This situation represents a system of equations.

⭐What is a system of equations?

• A system of equation is two or more equations that intersect at a point (x,y)

⭐ What are the two equations for this situation?

• To make the 2 equations for this situation, we need to declare what the variables are.

Pigs and chickens have 1 head, so let's create the equation:

`x + y = 70`

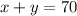
This equation represents the number of heads present

Let x = the number of pigs, and let y = the number of chickens

Pigs have 4 legs, while chickens have 2 legs, so let's create the equation:

`4x + 2y = 200`

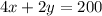
The equation represents the number of legs present

⭐Now that we made the two equations, let's solve the system of equations.

⭐How do you solve a system of equations?

• Elimination
• Substitution
• Graphing

In this case, substitution is the best way we can solve this system of equations.

⭐How do we solve a system using substitution?

• You take one equation, set it equal to one variable, and literally substitute said variable into another equation, and solve for another variable.

To understand substitution, I'll demonstrate it here with our system:

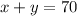`x+y = 70` . . . . (1)

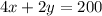`4x + 2y = 200` . . . . (2)

Set equation 1 equal to "y" so we can solve for "x":

`y = 70 -x`

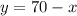
Substitute "y" into equation 2:

`4x+2y = 200`

`4x + 2(70-x)= 200`

`4x + 140 -2x = 200`

`2x + 140 = 200`

`2x = 60`

`x = 30`

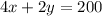
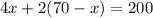
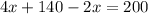
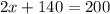
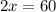
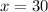
∴ There are 30 pigs on the farm.

Substitute "x" back into equation 1 to solve for "y":

`x+y = 70`

`30 + y = 70`

`y = 40`

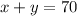
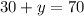
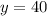
∴ There are 40 chickens on the farm.