Question

#50. The figure below is composed of four semicircles on the sides of a square. If the square had an area if 64, What is the length of the darkened outline of the figure? F. 8pi G. 16pi H.24pi J.32Pi K.64pi. Please explain?

Answer 1

G. 16π

Explanation:

Let's define the terms we see in the problem to understand how to solve it.

⭐What is the area of a square?

• 
  `area = side^2`
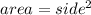
• the sides of a square are congruent (the same)

⭐What is the circumference of a circle?

• 
  `circumference = pi*diameter`
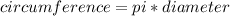
• the "perimeter" of a circle

Each side of the square is the diameter of the semicircle.

The circumference of the semicircle is half of the circumference of the circle the semicircle is part of.

Therefore, we can find 1/2 of the circumference of each semicircle and add them up to find the length of the darkened outline.

First, let's find the length of each side of the triangle.

`area = side^2`

`64 = side^2`

`√(64) = √(side^2)`

`8 = side`

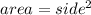
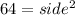
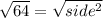
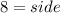
∴ Each side length of the square is 8.

As each side length of the square is the diameter of each semicircle, need to take 1/2 of the circumference of one semicircle.

We are taking 1/2 of the circumference of only one semicircle because each semicircle will have the same circumference if they have the same diameter.

`circumference = pi*diameter`

`circumference = 8pi`

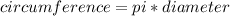
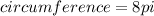
1/2 of the circumference:

`4pi`

Multiply 1/2 of the circumference by 4, because there are 4 semicircles:

`4pi*4 = 16pi`

∴ The length of the darkened outline of the figure is 16π