Explanation:
x^(a/b)
means
![\sqrt[b]{ {x}^(a) }](https://img.qammunity.org/2023/formulas/mathematics/high-school/l99iz4ht56kip6k08w93shertwo9cey784.png)
the numerator of the exponent is the actual "to the power of" factor.
the denominator defines the degree of the root to be taken.
as any integer number is also a fraction like
6 = 6/1
this applies to any form of rational numbers like
x^0.25 = x^(25/100) = x^(1/4) =
![\sqrt[4]{ {x}^(1) } = \sqrt[4]{x}](https://img.qammunity.org/2023/formulas/mathematics/high-school/kvqtiypzy4rvjnq5t3xqhzk552g2yzmmru.png)
with irrational numbers as exponents this gets trickier, as with infinite numbers without a pattern after the decimal point we have a problem to precisely specify the degree of the root, as we also have a problem to specify the irrational number itself.
we try to find the origin of the irrational number (like a square root)
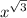
or
![\sqrt[ √(3) ]{ {x}^(2) } = {x}^(2 / √(3) )](https://img.qammunity.org/2023/formulas/mathematics/high-school/ekgcuta3w8yti73ht0w06mz6jdbx4shbqz.png)
so,
![√(2) = \sqrt[2]{2} = {2}^(1 / 2)](https://img.qammunity.org/2023/formulas/mathematics/high-school/7jbfx88kdlycam4i3x4va25vsldbfuuz45.png)