Correct Question:-
Solve the following differential equation using Laplace transformation.
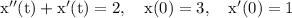
where
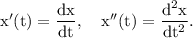

Solution:-
Let,
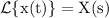
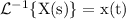
Given,
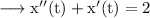
We take Laplace transformation of both sides of the equation.
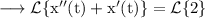
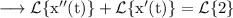
We have,
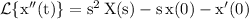
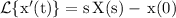
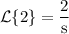
Then,
![\small\text{$\longrightarrow\rm{\big[s^2\,X(s)-s\,x(0)-x'(0)\big]+\big[s\,X(s)-x(0)\big]=(2)/(s)}$}](https://img.qammunity.org/2023/formulas/mathematics/high-school/t1jmlgy22wcuanqgdmewwkoism31v3rulc.png)
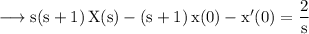
Given that
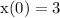 and
and
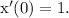 Then,
Then,
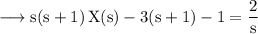
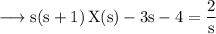
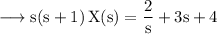
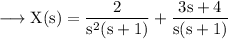
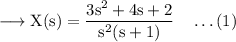
We will factorise this expression by partial fractions.
Assume,
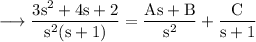
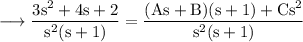
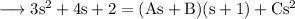
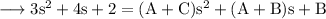
Equating corresponding coefficients,
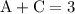
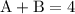
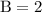
Solving each equation we get,
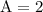
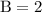
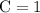
Therefore,
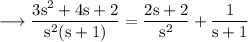
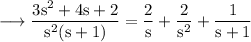
Then (1) becomes,
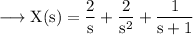
Now we will inverse Laplace transformation to obtain the solution.
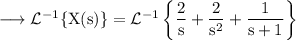
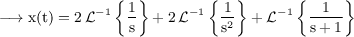
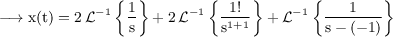
We have,
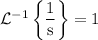
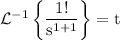
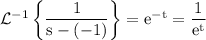
Hence,
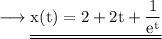
This is the solution to our differential equation.

Some results of Laplace Transformation:-
