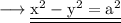When X and Y axes are rotated through an angle θ to form X' and Y' axes, then the relation between the axes and the angle is given by,
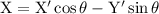

Then x and y are replaced in terms of x' and y' as,
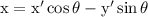
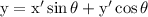
Here θ = π/6. Then,
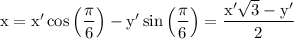

We are asked to find the transformed equation for,
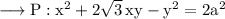
We will give substitutions for x and y to find it.
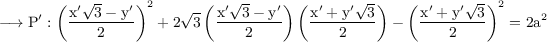
Simplify this equation to get,
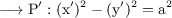
Hence the transformed equation is,