Explanation:
A number is divisible by 11 if and only if the difference between sum of alternate digits is divisible by 11.
Here the number is x557x55. The difference between the sum of alternate digits is,

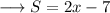
By statement, the number x557x55 is divisible by 11 if and only if
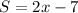 is divisible by 11.
is divisible by 11.
Let,
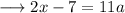
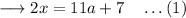
We separate the RHS as the following.
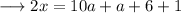
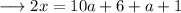

In this question, the LHS is an even integer since x is a digit, i.e., integer. So RHS should also be an even integer.
Since
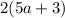 is even,
is even,
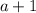 must be even. So let,
must be even. So let,

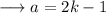
Then (1) becomes,
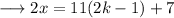
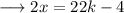
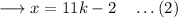
So this is expression for x, for any integer k.
As x is a digit of x557x55, x is a single digit integer, so its value lies in between 1 and 9 [x ≠ 0 because it is also the left most digit of x557x55], i.e.,

From (2),
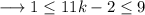
Adding 2,
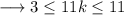
Dividing by 11,

Since k is an integer, we get,

Then from (2),
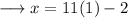
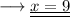
Hence the value of x is 9.