Explanation:
The general quadratic equation
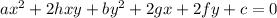 represents pair of straight lines if its discriminant
represents pair of straight lines if its discriminant
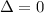 and
and
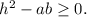 The discriminant of this equation is given by the determinant,
The discriminant of this equation is given by the determinant,
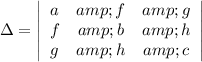
Here the given equation is,
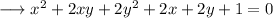
So,
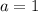
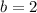
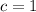
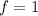
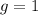
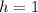
Thus,
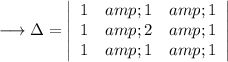
Performing the operation
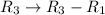 over this determinant,
over this determinant,
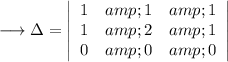
Now the 3rd row is completely so the discriminant is equal to zero.

So our equation represents degenerate conics, which are,
pair of distinct straight lines intersecting each other at any point if
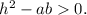
pair of straight lines, either coincident or distinct but parallel to each other, if
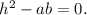
a single point if
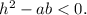
We see that,
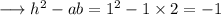

So our equation represents a single point.
Hence the equation does not represent pair of straight lines.