Answer:
The tightened spot is 10 feet away from the foot of the pole.
Explanation:
1. Draw the diagram. Notice that the shape of the electric pole and its supporting wire creates a right triangle.
2. We know 2 side lengths already (26ft, 24ft), and we need to find 1 more side length. Therefore, to find the 3rd side length of a right-triangle, utilize Pythagoras' Theorem.
⭐What is the Pythagoras' Theorem?
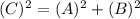
- An equation to find a 3rd side length
- C = hypotenuse
- A = one leg
- B = another leg
3. Substitute the values of the side lengths into the equation, and solve for the unknown side length.
Let B= the distance from the tightened spot to the foot of the pole.
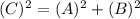
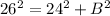
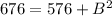
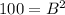
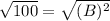
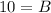
∴ The tightened spot is 10 feet away from the foot of the pole.
Diagram: