Question

NO LINKS!!!

The model t = 16.708 ln(x/(x-705)) approximates the term of a mortgage of $150,000 at 6% interest rate, where t is the term of the mortgage in years and x is the monthly payment plan in dollars.

a. Approximate in terms (in yr) of a $150,000 mortgage at 6% when the monthly is $897.72 and when the monthly payment is $1526.49 (Round your answers to the nearest whole number).
$897.72 ________ yr
$1526.49_________ yr

b. Approximate the total amounts paid (in dollars) over the term of the mortgage with a monthly payment plan of $897.72 and with a monthly payment plan of $1526.49. (Round your answers to 2 decimal places.)
$897.72 $_____________
$1526.49 $_____________

What is the amount of the total is interest costs (in dollars) in each case? (Round your answers to 2 decimal places)
$897.72 $__________
$1526.49 $__________

c. What is the vertical asymptote for the model? ____________

Interpret its meaning in the context of the problem.
The monthly payment must be (more or less) than $________, and the close to this value is, the (quicker you will be able or longer it will take) to pay off the mortgage.

Answer 1

(a) $897.72: 26 yr

$1526.49: 10 yr

(b) See below.

(c) x = 705

more, $705, longer it will take

Explanation:

Given equation:

`t=16.708 \ln \left((x)/(x-705)\right)`

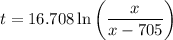
where:

• t = term of the mortgage (in years)
• x = monthly payment plan (in dollars)

Part (a)

`\begin{aligned}x=897.72 \implies t& =16.708 \ln \left((897.72)/(897.72-705)\right)\\& =16.708 \ln \left(4.65815691...\right)\\&=16.708(1.53861985...)\\&=25.70726...\\&=26\; \rm years\end{aligned}`

`\begin{aligned}x=1526.49 \implies t& =16.708 \ln \left((1526.49)/(1526.49-705)\right)\\& =16.708 \ln \left(1.85819669...\right)\\& =16.708(0.619606496...)\\&=10.352385...\\&=10 \; \rm years\end{aligned}`

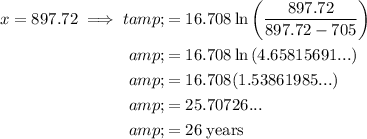
Part (b)

To approximate the total amounts paid (in dollars) over the term of the mortgage, multiply the monthly payment by the term.

Please note I have provided two calculations per monthly payment:

(1) by using the exact term, and (2) using the rounded term from part (a).

`\implies \$897.72 * 25.7072605... * 12 =\$276935.06`

`\implies \$897.72 * 26 * 12=\$280088.64`

`\implies \$1526.49 * 10.3523853... * 12=\$189633.75`

`\implies \$1526.49 * 10 * 12 =\$183178.80`

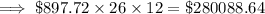
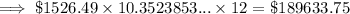
To calculate the amount of interest costs (in dollars) in each case, subtract $150,000 from the total amounts paid:

`\$897.72\implies 276935.06-150000=\$126935.06`

`\$897.72 \implies 280088.64-150000=\$130088.64`

`\$1526.49 \implies 189633.75-150000=\$39633.75`

`\$1526.49\implies 183178.80-150000=\$33178.80`

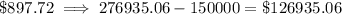
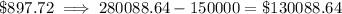
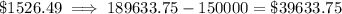
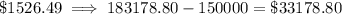
Part (c)

The natural logarithm of a negative number cannot be taken.

Therefore, x > 705.

So the vertical asymptote for the model is:

• x = 705

The monthly payment must be more than $705, and the closer to this value the payment is, the longer it will take to pay off the mortgage.