Question

Solve the logarithmic equation. log 10 (x raise to power 2 - 4x )=2​

Answer 1

`x=2+2√( 26)`

`x=2-2√( 26)`

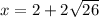
Explanation:

Given logarithmic equation:

`\log_(10)(x^(2)-4x)=2`

`\textsf{Apply log law}: \quad \log_ab=c \iff a^c=b`

`\implies 10^2=x^2-4x`

`\implies 100=x^2-4x`

`\implies x^2-4x=100`

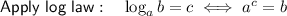
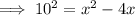
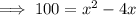
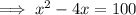
Add the square of half the coefficient of the term in x to both sides of the equation:

`\implies x^2-4x+\left((-4)/(2)\right)^2=100+\left((-4)/(2)\right)^2`

`\implies x^2-4x+\left(-2\right)^2=100+\left(-2}\right)^2`

`\implies x^2-4x+4=100+4`

`\implies x^2-4x+4=104`

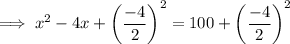
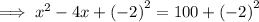
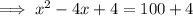
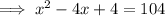
Factor the perfect square trinomial on the left side of the equation:

`\implies (x-2)^2=104`

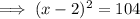
Square root both sides:

`\implies x-2=\pm √(104)`

`\implies x-2=\pm √(4 \cdot 26)`

`\implies x-2=\pm √(4) √( 26)`

`\implies x-2=\pm 2√( 26)`

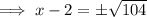
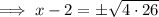
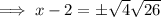
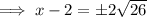
Add 2 to both sides:

`\implies x=2\pm 2√( 26)`

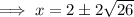
Therefore, the solutions are:

• 
  `x=2+2√( 26)`

• 
  `x=2-2√( 26)`