Question

Let K=
`20^(20)`.Suppose that
`(20^(k) )/(k^(20) ) =20^(n)`.find the largest power of 20 that divides n?

Answer 1

20^2 = 400, the 2nd power of 20

Explanation:

Given that k=20^20 and 20^k/k^20 = 20^n, you want the largest power of 20 that divides n.

Logarithms

Taking the base-20 logarithm of both equations, we have ...

`log_20(k)=\log_(20){20^(20)}\ \Longrightarrow\ log_20(k)=20\\\\\log_(20){(20^k)/(k^(20))}=log_20(20^n)\ \Longrightarrow\ k-20log_20(k)=n`

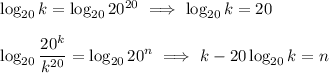
Substituting for k and log(k), we get ...

`20^(20) -20\cdot20=n\\\\20^2(20^(18)-1)=n`

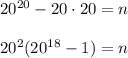
This shows us the largest power of 20 that is a factor of n is 20².