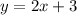Question

Does someone mind helping me with this? Thank you!

Answer 1

`y = 2x - 3`

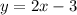
Explanation:

❗ The way I solved this problem doesn't involve me using point-slope form like the problem tells you to use❗

⭐ Perpendicular lines have a slope that is the opposite reciprocal of the slope of the line it is perpendicular to

⭐What does "opposite reciprocal" mean?

• Opposite reciprocal: the slope of the perpendicular line is the reciprocal of the slope of the line it is perpendicular to and it has the opposite sign of the slope of the line it is perpendicular to.

⭐What is slope-intercept form?

• One way to write the equation of a line

• 
  `y = mx + b`
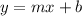
• m = the slope
• b = the y-intercept

We can find the equation of the perpendicular line by:

1. Substituting the slope of the perpendicular line into the point-slope form equation using the opposite reciprocal
2. Substituting the given coordinate into the point-slope form equation to solve for b

1. Substituting the slope into the point-slope form equation:

⭐ Perpendicular lines have a slope that is the opposite reciprocal of the slope of the line it is perpendicular to

The slope of the line the perpendicular like is perpendicular to is
`(-1)/(2)`.

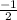Therefore, the slope of the perpendicular line is
`2`

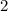
Substitute the slope into the point-slope form equation.

`y = 2x + b`

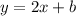
Now, all we have to do is solve for b.

2. Substituting the given coordinate into the point-slope form equation:

We are given the coordinate (6,9).

`y = 2x + b`

`9 = 2(6) + b`

`9 = 12 + b`
`-3 = b`

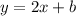
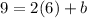
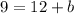
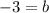
Substitute "b" into the point-slope form equation.

`y = 2x + 3`