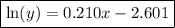Question

NO LINKS!!

The approximate lengths and diameters (in inches) of bright common wire nails are shown in the table. Find a logarithmic equation that relates the diameter y of a bright common wire nail to its length x. (Use the first and last lengths and diameters to form the equation. Round your answers to three decimal places.)

ln(y)=

Length, x Diameter, y
2. 0.113
3. 0.151
4. 0.192
5. 0.222
6. 0.262

Answer 1

`\ln (y) = 0.210x-2.601`

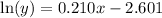
Explanation:

Given table:

`\begin{array}c\cline{1-2} \sf Length & \sf Diameter \\x & y\\\cline{1-2} \vphantom{\frac12} 2 & 0.113\\\cline{1-2} \vphantom{\frac12} 3& 0.151\\\cline{1-2} \vphantom{\frac12} 4& 0.192\\\cline{1-2} \vphantom{\frac12} 5& 0.222\\\cline{1-2} \vphantom{\frac12} 6& 0.262\\\cline{1-2} \end{array}`

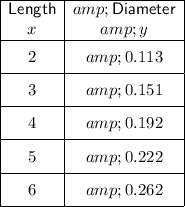
To convert y = abˣ to linear form, take natural logs of both sides and rearrange:

`\begin{aligned}y=ab^x \implies \ln y &= \ln ab^x\\\implies \ln y &= \ln a + \ln b^x\\\implies \ln y &= \ln a + x \ln b\\\implies \ln y &=x \ln b+ \ln a\end{aligned}`

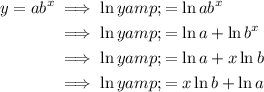
This is in the straight-line form y = mx + c.

Substitute the first and last values of x and y from the table into the natural log formula:

• 
  `\ln 0.113 = 2 \ln b+\ln a`

• 
  `\ln 0.262 = 6 \ln b+\ln a`

Subtract the first equation from the second equation to eliminate ln(a);

`\implies \ln 0.262 - \ln 0.113 = 6 \ln b - 2 \ln b`

`\implies \ln 0.262 - \ln 0.113 = 4 \ln b`

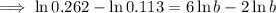
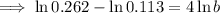
Apply the quotient log law:

`\implies \ln (0.262)/(0.113) = 4\ln b`

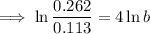
Rearrange and solve for ln(b):

`\implies \ln b = (1)/(4)\ln (0.262)/(0.113)`

`\implies \ln b = 0.210\; \sf (3\;d.p.)`

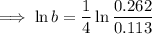
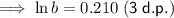
Substitute the found value of ln(b) into one of the equations and solve for ln(a):

`\implies \ln 0.262 = 6 \cdot (1)/(4)\ln (0.262)/(0.113)+\ln a`

`\implies \ln a=\ln 0.262 -(6)/(4)\ln (0.262)/(0.113)`

`\implies \ln a = -2.601\; \sf (3\;d.p.)`

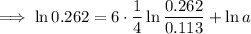
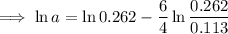
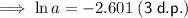
Substitute the found values of ln(a) and ln(b) into the formula to create an equation for ln(y):

`\boxed{\ln (y) = 0.210x-2.601}`