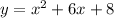Question

Write an equation for the parabola when the x intercepts are (-2,0) and (-4,0)

Answer 1

`y = x^2 + 6x + 8`

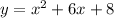
Explanation:

⭐What is the equation of a parabola in standard form?

• 
  `y = ax^2 + bx + c`

⭐Whenever you factorise a quadratic (parabola), you are writing the parabola in terms of its x-intercepts.

⭐ Therefore, the expressions of the x-intercepts are the factors of your quadratic.

⭐What are factors of a number?

• factors are 2 or more numbers or expressions that multiply together to become a number

We have to reverse-engineer this problem to find the quadratic by:

1. re-writing the quadratic in terms of its factors (the x-intercepts)
2. multiplying the factors
3. simplifying the product from step #2

1. Re-write the quadratic in terms of its factors

If one of the x-intercepts is -2, then the expression for said x-intercept is:
`(x+2)`

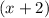
If one of the x-intercepts is -4, then the expression for said x-intercept is:

`(x+4)`

2. Multiply the factors

`y = (x+2)(x+4)`

`y = x^2 + 4x + 2x + 8`

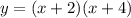
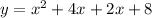
3. Simplify the products

`y = x^2 + 6x + 8`