Question

Keegan bought 5 T-shirts and 2 pairs of shoets for $49.50. Each pair of shorts, s, cost twice as much as each T-shirt, t.

Part A
Which system ot equations can vevused to find the price of the shorts and t-shirts?
(use attachment)

Part B
how much did keegan pay for each t-shirt and each pair of shorts?
​

Answer 1

A)
`{2s + 5t = 49.50\\\\s = 2t`

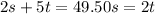
B) Keegan paid $5.50 for each t-shirt and $11 for each short.

Explanation:

A)

⭐ What is a system of equations?

• A system of equations is two or more equations that intersect at a common point (x,y)

We are asked to create a system of equations for Keegan's situation.

Let s = the price for every short

Let t = the price for every t-shirt

So, if Keegan buys 2 shorts and 5 t-shirts, his cost will be $49.50.

As an equation, this situation would be:

`2s + 5t = 49.50`

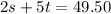
It's given that the cost of 1 short is twice the cost of 1 t-shirt.

As an equation, this situation would be:

`s = 2t`

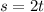
B)

⭐How can we solve a system of equations?

• You can solve a system of equations by substitution
• You can solve a system of equations by graphing
• You can solve a system of equations by elimination

For this problem, the best way to solve this system of equations is through substitution. I will demonstrate how to use substitution for this problem.

Using the equations
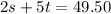`2s + 5t = 49.50` and
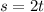`s = 2t`, we will literally substitute a variable from one equation into another equation to solve for the other variable.

Given that
`s = 2t`:

`2s + 5t = 49.50`

`2(2t) + 5t = 49.50`

`4t + 5t = 49.50`

`9t = 49.50`

`t = 5.50`

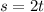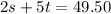
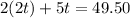
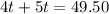
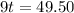
∴ It costs Keegan $5.50 for one t-shirt.

Now, we can substitute the value of t into the same equation to solve for the value of s.

Given that
`t = 5.50`:

`2s + 5(5.50) = 49.50`

`2s + 27.5 = 49.50`

`2s = 22`

`s = 11`

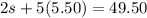
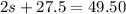
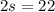
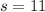
∴ It costs Keegan $11 for one short.