Question

A 45 kg mass is dragged 50 m over a surface. If 1.0 kW of power is produced over 10 seconds,

what is the coefficient of friction for the surface?

Answer 1

Approximately
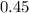`0.45` (assuming that the surface is level, the mass is moving at constant velocity, and that
`g = 9.81\; {\rm m\cdot s^(-2)}`.)

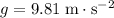Step-by-step explanation:

With a power of
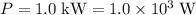`P = 1.0\; {\rm kW} = 1.0* 10^(3) \; {\rm W}`, the work that would be done over
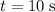`t = 10\; {\rm s}` would be:

`\begin{aligned}(\text{work}) &= (\text{power})\, (\text{time}) \\ &= (1.0* 10^(3)\; {\rm W})\, (10\; {\rm s}) \\ &= 1.0 * 10^(4)\; {\rm J}\end{aligned}`.

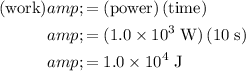Divide work by distance to find the force that did the work:

`\begin{aligned} (\text{force}) &= \frac{(\text{work})}{(\text{distance})} \\ &= \frac{1.0* 10^(4)\; {\rm J}}{50\; {\rm m}} \\ &= 200\; {\rm N}\end{aligned}`.

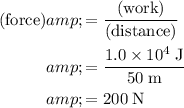If this mass is moving at a constant velocity, the magnitude of friction on this mass will be equal to that of the external force,
`200\; {\rm N}`.

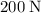If the surface is level, the magnitude of the normal force on this mass will be equal to that of weight:

`\begin{aligned}(\text{weight}) &= (\text{mass})\, g \\ &= (45\; {\rm kg})\, (9.81\; {\rm N\cdot kg^(-2)}) \\ &\approx 4.41 * 10^(3)\; {\rm N}\end{aligned}`.

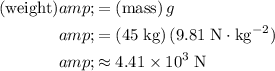Divide the magnitude of friction by normal force to find the coefficient of friction:

`\begin{aligned}& (\text{coefficient of friction}) \\ =\; & \frac{(\text{friction})}{(\text{normal force})} \\ \approx\; & \frac{200\; {\rm N}}{(45\; {\rm kg})\, (9.81\; {\rm N\cdot kg^(-1)}))} \\ \approx \; & 0.45\end{aligned}`.