Question

A semi-circle has an area of 50 m². Find the perimeter of the semi-circle. Give your answer correct to one decimal place.​

Answer 1

29.0 m

Explanation:

`\boxed{\begin{minipage}{4cm}\underline{Area of a semicircle}\\\\$A=(1)/(2)\pi r^2$\\\\where:\\\phantom{ww}$\bullet$ $r$ is the radius\\ \end{minipage}}`

Given the area of the semicircle is 50 m², substitute this into the formula and rearrange to isolate r:

`\begin{aligned}\implies(1)/(2)\pi r^2&=50\\\pi r^2 & = 100\\r^2 & = (100)/(\pi)\\r&=\sqrt{(100)/(\pi)}\end{aligned}`

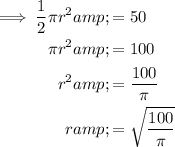
The perimeter of a semicircle is the sum of the diameter of the circle and half its circumference.

• Diameter of a circle = 2r
• Circumference of a circle = 2πr

Therefore:

`\begin{aligned}\textsf{Perimeter of a semicircle}&=2r+\pi r\\&=r(2+\pi)\\&=\sqrt{(100)/(\pi)}(2+\pi)\\&=29.0083301...\end{aligned}`

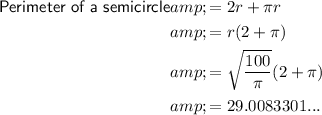
Therefore, the perimeter of the semicircle is 29.0 m (1 d.p.).