Answer:
First 6 terms: 4, 9, 14, 19, 24, 29, ...
First differences: +5, +5, +5, +5, +5
Second differences: +0, +0, +0, +0
Linear model
Explanation:
A recursive formula for an arithmetic sequence allows you to find the nth term of the sequence provided you know the value of the previous term in the sequence.
Given recursive formula:
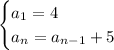
Calculate the first 6 terms of the sequence:
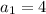
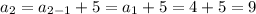
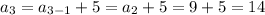
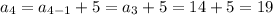
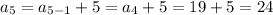
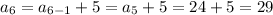
Therefore, the first 6 terms of the sequence are:
- 4, 9, 14, 19, 24, 29, ...
Calculate the first differences between the terms:
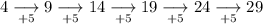
Calculate the second differences (i.e. the differences between the first differences):
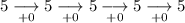
As the first differences are constant and the second differences are zero, the sequence is a linear model.