Question

NO LINKS!!!

Assume that the following statement, S_k, is true:
A factor of (2^(2k-1) + 3^(2k-1)))is 5.
Show that for each integer k ≥ 1, if S_k is true, then S_(k+1) is true.
2^2(k + 1) - 1)) + 3^2(k + 1) - 1)) = 2^(2k + ____) - 1)) + 3^2k + ___) - 1))
= 2^(2k - 1) * 2^(___) + 3^(2k - 1) * 3^(___)
= ______ * 2^(2k-1) + ______ * 3^(2k-1)
= (2^(2k-1) + 3^(2k-1)) + (2^(2k-1) + 3^(2k-1)) + (2^(2k-1) + (3^(2k-1) + ______*3^(2k-1)

Hence, S_k+1 is true or false, which completes the inductive step and the proof by the mathematical induction.

Answer 1

It is assumed the statement is true for
`S_k`:

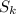• A factor of
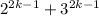  `2^(2k-1)+3^(2k-1)` is 5.

Show that
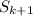`S_(k+1)` is also divisible by 5:

• 
  `2^(2(k+1)-1)+3^(2(k+1)-1)=`
• 
  `2^(2k+2-1)+3^(2k+2-1)=`
• 
  `2^((2k-1)+2)+3^((2k-1)+2)=`
• 
  `2^(2k-1)*2^2+3^(2k-1)*3^2=`
• 
  `4*2^(2k-1)+9*3^(2k-1)=`
• 
  `4*2^(2k-1)+4*3^(2k-1)+5*3^(2k-1)=`
• 
  `4(2^(2k-1)+3^(2k-1))+5*3^(2k-1)`

The first part is divisible by 5 as we assumed in the beginning and the second part has a factor of 5 so the sum is divisible by 5.

Hence it makes
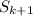`S_(k+1)` true, so the proof is complete.