Question

NO LINKS!!

A principal P, invested 9.5% compounded continuously, increases to an amount K times the original principal after t years, where t = ln(K)/0.095.

a. Complete the table. (Round your answers to one decimal place)

K t
1
2
3
4
6
8
10
12


b. Sketch the graph of the function.

Answer 1

`\begin{array}c\cline{1-2}\vphantom{\frac12} K & t\\\cline{1-2} \vphantom{\frac12} 1 & 0\\\vphantom{\frac12} 2 & 7.3\\\vphantom{\frac12} 3&11.6 \\\vphantom{\frac12} 4& 14.6\\\vphantom{\frac12} 6&18.9 \\\vphantom{\frac12} 8& 21.9\\\vphantom{\frac12} 10& 24.2\\\vphantom{\frac12} 12&26.2\\ \cline{1-2}\end{array}`

See attachment for the graph.

Explanation:

Part (a)

Given equation for t:

`t=(\ln (K))/(0.095)`

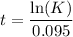
Substitute the given values of K into the equation for t and round the answers to one decimal place:

`\begin{array}\cline{1-2}\vphantom{\frac12} K & t\\\cline{1-2} \vphantom{\frac12} 1 & 0\\\vphantom{\frac12} 2 & 7.3\\\vphantom{\frac12} 3&11.6 \\\vphantom{\frac12} 4& 14.6\\\vphantom{\frac12} 6&18.9 \\\vphantom{\frac12} 8& 21.9\\\vphantom{\frac12} 10& 24.2\\\vphantom{\frac12} 12&26.2\\ \cline{1-2}\end{array}`

Part (b)

To sketch the graph of the given function (see attachment):

• Plot the values of K along the x-axis.
• Plot the values of t along the y-axis.
• Plot the points from the table from part (a).
• Draw a curve through the plotted points.