Answer:
$44,334.34
Explanation:

Given:
- P = $6000
- r = 5.0% = 0.05
- t = 40 years
Substitute the given values into the continuous compounding formula and solve for A:
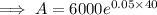
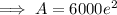
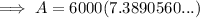
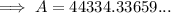
Therefore, the balance of the account after 40 years will be $44,334.34 (nearest cent).