Question

In right triangle ABC, altitude CD with length h is drawn to its hypotenuse. We also know AD = 12 and DB=3. What is the length of h?

Only sides/angles known are
Base= 12+3,
Angle= Right angle/90°.
No clue how to solve this. I tried many methods. everyone who’s asked this question on here did not get a good answer. Please explain how it is done and what theorem is used.

Answer 1

h = 6

Explanation:

h is the short leg for AD in ΔADC: AD = 12

h is the long leg for DB in ΔCDB: DB = 3

Hence:

12/h = h/3

3 * 12/h = 3 * h/3 ==> isolate h by multiplying 3 on both sides

36/h = h

h * 36/h = h*h ==> multiply by h on both sides to remove fractions

36 = h^2

h =
`√(36)`

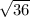
h = 6