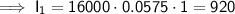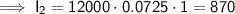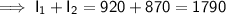Question

NO LINKS!!

A total of $28000 is invested in 2 municipal bonds that pay 5.75% and 7.25% simple interest. The investor wants an annual interest income of $1790 from the investments. What amount should be invested in the 5.75% bond?

Answer 1

$16,000

Explanation:

Simple Interest Formula

I = Prt

where:

• I = Interest accrued
• P = Principal amount
• r = Interest rate (in decimal form)
• t = Time (in years)

Let investment 1 be the bond that pays 5.75% simple interest.

Let investment 2 be the bond that pays 7.25% simple interest.

Given:

• P₁ + P₂ = $28,000
• r₁ = 5.75% = 0.0575
• r₂ = 7.25% = 0.0725
• t = 1 year

Create two equations for the interest from both investments.

Interest from Investment 1

`\implies \sf I_1=P_1 \cdot 0.0575 \cdot 1`

`\implies \sf I_1=0.0575\:P_1`

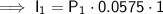
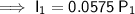
Interest from Investment 2

`\implies \sf I_2=P_2 \cdot 0.0725 \cdot 1`

`\implies \sf I_2=(28000-P_1)0.0725`

`\implies \sf I_2=2030-0.0725\:P_1`

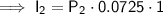
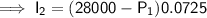
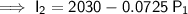
Given that the sum of the interest from both investments is $1,790:

`\implies \sf I_1+I_2=1790`

`\implies \sf 0.0575\:P_1+2030-0.0725\:P_1=1790`

`\implies \sf -0.015\:P_1=-240`

`\implies \sf P_1=16000`

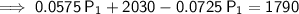
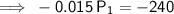
Therefore, $16,000 should be invested in the 5.75% bond.

Check:

`\implies \sf I_1=16000 \cdot 0.0575 \cdot 1 = 920`

`\implies \sf I_2=12000 \cdot 0.0725 \cdot 1 = 870`

`\implies \sf I_1+I_2=920+870=1790`