Question

Answer for the page? ​

Answer 1

(9) x = 9

(10) I cannot see the image clearly, sorry :(

(11) x = 54

(12) I cannot see the image clearly, sorry :(

(13) ∠P = 64°

(14) ∠Q = 26°

(15) ∠U = 47°

(16) ∠W = 43°

Explanation:

(9)

To find an unknown side length in a right triangle, we need to use a trigonometric function.

⭐ What is a trigonometric function?

• A trigonometric function is the ratio of two side lengths for a certain angle, where one of the side lengths is unknown and denoted by a variable (x)

⭐ What are the trigonometric functions?

• sin(θ) = opposite/hypotenuse
• cos(θ) = adjacent/hypotenuse
• tan(θ) = opposite/adjacent
• θ = an angle measure that isn't the 90 degrees angle.

To determine which trigonometric function to use, we need to see which type of side lengths we are given (hypotenuse/opposite/adjacent).

We are given side length x, which is opposite of the 37 degrees, and side length 15, which is the hypotenuse of the triangle. Therefore, we will use sin(θ).

Substitute the angle measure we are given and the side lengths into sin(θ).

`sin(37) = (x)/(15)`

`15sin(37) = x`

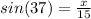
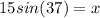
Compute this equation into a scientific calculator. I recommend using the Desmos Scientific Calculator.

`9.0 = x`

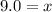
(10) I'd need to see x clearly to solve.

(11) To find an unknown side length in a right triangle, we need to use a trigonometric function.

⭐ What is a trigonometric function?

• A trigonometric function is the ratio of two side lengths for a certain angle, where one of the side lengths is unknown and denoted by a variable (x)

⭐ What are the trigonometric functions?

• sin(θ) = opposite/hypotenuse
• cos(θ) = adjacent/hypotenuse
• tan(θ) = opposite/adjacent
• θ = an angle measure that isn't the 90 degrees angle.

To determine which trigonometric function to use, we need to see which type of side lengths we are given (hypotenuse/opposite/adjacent).

We are given side length x, which is the hypotenuse of the triangle, and side length 14, which is adjacent to the 75 degrees. Therefore, we will use cos(θ).

Substitute the angle measure we are given and the side lengths into cos(θ).

`cos(75) = (14)/(x)`

`(14)/(cos(75)) = x`

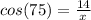
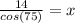
Compute this equation into a scientific calculator. I recommend using the Desmos Scientific Calculator.

`54 = x`

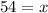
(12) I'd need to see x clearly to solve.

(13) To find the angle measure of an angle in a right angle triangle, we need to use the inverses of the trigonometric functions.

⭐ What are the inverses of the trigonometric functions?

• 
  `sin^-1(opposite/hypotenuse) =`
• 
  `cos^-1(adjacent/hypotenuse) =`
• 
  `tan^-1(opposite/adjacent)`

First, we need to see the type of side lengths we are given (adjacent/hypotenuse/opposite) to determine which inverse trigonometric function we use for each angle.

∠P is adjacent to side length 8, and side length 18 is the hypotenuse of the triangle. Therefore, we will use
`cos^-1(adjacent/hypotenuse) =`.

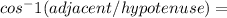Substitute the side lengths and compute using a scientific calculator. I recommend using the Desmos Scientific Calculator.

`cos^-1((8)/(18))`

∴ ∠P = 64°

(14) To find the angle measure of an angle in a right angle triangle, we need to use the inverses of the trigonometric functions.

∠Q is opposite of side length 8, and side length 18 is the hypotenuse of the triangle. Therefore, we will use
`sin^-1(opposite/hypotenuse) =`.

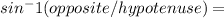Substitute the side lengths and compute using a scientific calculator.

`sin^-1((8)/(18))`

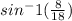
∴ ∠Q = 26°

(15) To find the angle measure of an angle in a right angle triangle, we need to use the inverses of the trigonometric functions.

∠U is opposite of side length 11, and side length 15 is the hypotenuse of the triangle. Therefore, we will use
`sin^-1(opposite/hypotenuse) =`.

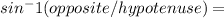Substitute the side lengths and compute using a scientific calculator.

`sin^-1((11)/(15))`

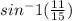
∴ ∠Q = 47°

(16) To find the angle measure of an angle in a right angle triangle, we need to use the inverses of the trigonometric functions.

∠W is adjacent to side length 11, and side length 15 is the hypotenuse of the triangle. Therefore, we will use
`cos^-1(adjacent/hypotenuse) =`.

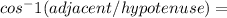Substitute the side lengths and compute using a scientific calculator.

`cos^-1((11)/(15))`

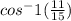
∴ ∠W = 43°