Answer:
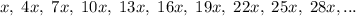
Explanation:

Given:
Substitute the given values of a and d into the formula to create an equation for the nth term:
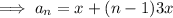
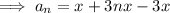
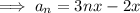
To find the first 10 terms of the given arithmetic sequence, substitute n = 1 through 10 into the equation.
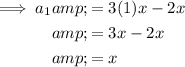
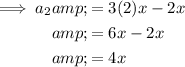
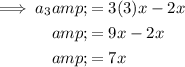
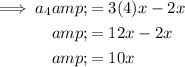
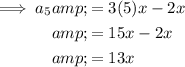
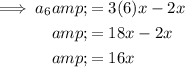
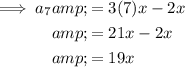
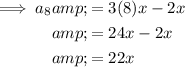
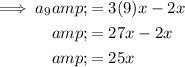
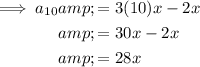
Therefore, the first 10 terms of the given arithmetic sequence are: