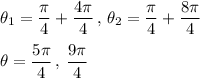Question

Which is the solution of 2cos theta = 2 sin theta for pi ≤ theta ≤ 3 pi

THIS IS SO CONFUSING MAN HELP

Answer 1

`\displaystyle{\theta=(5\pi)/(4)\, , \, (9\pi)/(4)}`

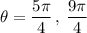
Explanation:

Given the equation
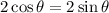`\displaystyle{2\cos \theta = 2\sin \theta}`. We have to divide both sides by 2 which gives us
`\displaystyle{\cos \theta = \sin \theta}`. Then divide both sides by
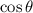`\displaystyle \cos \theta` which gives us
`\displaystyle{1=(\sin \theta)/(\cos \theta)}`.

We know that:

`\displaystyle{(\sin \theta)/(\cos \theta) = \tan \theta}`

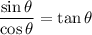
So we can rewrite the equation as
`\displaystyle{1=\tan \theta}`.

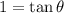We know that
`\displaystyle{\tan \theta = 1}` when
`\displaystyle{\theta = (\pi)/(4)+\pi k}` for
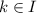`\displaystyle{k \in I}` (k is any integer). However, the equation is given with the interval
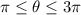`\displaystyle{\pi \leq \theta \leq 3\pi}`. Therefore, we have to substitute k-values that satisfy the interval.

It appears that only k = 1, 2 which gives us
`\displaystyle{\theta_1 = (\pi)/(4)+\pi}` and
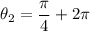`\displaystyle{\theta_2 = (\pi)/(4)+2\pi}`can be used since both satisfies both values and interval.

Simplifying both solutions:

`\displaystyle{\theta_1 = (\pi)/(4)+(4\pi)/(4) \, , \, \theta_2=(\pi)/(4)+(8\pi)/(4)}\\\\\displaystyle{\theta=(5\pi)/(4)\, , \, (9\pi)/(4)}`