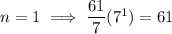Question

B)

Given that n is an integer greater than 1, explain why the largest prime factor of
2(7^n) - 2(7^n-1)+7^n+1 is 61.

Answer 1

See below.

Explanation:

Given expression:

`2(7^n) - 2(7^(n-1))+7^(n+1)`

`\textsf{Apply exponent rule} \quad a^b \cdot a^c=a^(b+c)`

`\implies 2(7^n) - 2(7^(n-1))+7^(n) \cdot 7^1`

`\textsf{Apply exponent rule} \quad (a^b)/(a^c)=a^(b-c)`

`\implies 2(7^n) - 2\left((7^(n))/(7^(1))\right)+7^(n)\cdot 7^1`

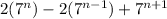
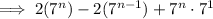
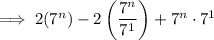
Simplify:

`\implies 2(7^n) - (2)/(7) (7^n)+7(7^(n))`

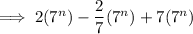
Factor out the common term 7ⁿ:

`\implies \left(2- (2)/(7) +7\right)7^(n)`

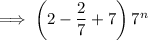
Therefore:

`(61)/(7)(7^n)`

A prime number is a whole number greater than 1 that cannot be made by multiplying other whole numbers. Therefore, the factors of a prime number are 1 and the number itself.

If n is an integer greater than 1, the number will always have at least 4 factors (1, 7, 61 and itself) and therefore cannot be a prime number by definition.

For example:

`n = 2 \implies (61)/(7)(7^2)=61 * 7=427`

`n = 3\implies (61)/(7)(7^3)=61 * 7^2=2989`

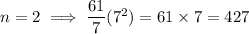
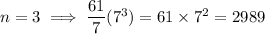
Therefore, the largest prime number is when n = 1:

`n = 1 \implies (61)/(7)(7^1)=61`