Answer:
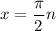 for n is any integers
for n is any integers
Explanation:
To know the asymptotes, first, we must know values of x that we turn y-value into an undefined value.
We know that:

Now we have to find value of x that turns the identity above into undefined value, and that is
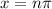 where n is any integers. (This gives 1/0 for all x = nπ)
where n is any integers. (This gives 1/0 for all x = nπ)
Therefore, a function
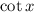 has asymptote lines at
has asymptote lines at
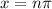 for n is integers.
for n is integers.
If we consider the given problem:
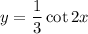
We have to find values of x that turn y-value undefined. We know that
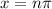 is asymptotes for
is asymptotes for
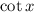 . Therefore,
. Therefore,
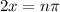 has to be asymptotes for
has to be asymptotes for
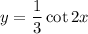 .
.
Hence, the asymptotes occur at
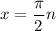 by solving the equation and for n is any integers.
by solving the equation and for n is any integers.