Answer:
Length of the base = 15 cm
Volume = 1125√2 cm³ = 1590.99 cm³ (2 d.p.)
Explanation:


If the lateral surface area (LSA) of the pyramid is three times the base area (BA):
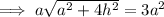
Rearrange the equation to isolate h²:

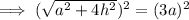
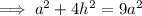
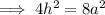
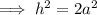

Given:
Substitute these values into the formula for the total surface area and solve for a:
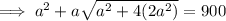
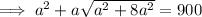
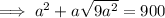
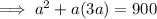
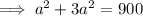
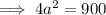
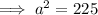
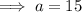
Therefore, the length of the base of the square based pyramid is:
To find the height (h), substitute the found value of a into the formula for h² and solve for h:
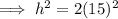
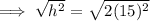
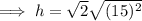
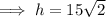
Therefore, the height of the square based pyramid is:

Given:
Substitute the values into the formula and solve for volume:
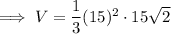
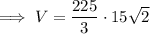
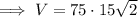
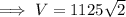
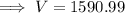
Therefore, the volume of the square based pyramid is: