Answer:
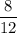
Explanation:
Let the unknown fraction be:
If the sum of the numerator and denominator is 20 then:
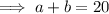
Rewrite the equation to isolate b:
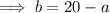
If the fraction is equal to 2/3 then:
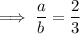
Cross multiply:
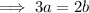
Substitute the expression for b into the cross-multiplied equation and solve for a:
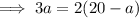
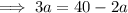
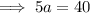
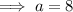
Substitute the found value of a into the equation for b and solve for b:
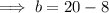
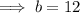
Therefore, the fraction for which the sum of the numerator and denominator is 20, and the value of the fraction is equal to 2/3 is: