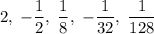Answer:
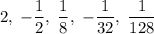
Explanation:

Given:
Substitute the given values of a and r into the formula to create an equation for the nth term:
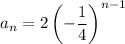
To find the first 5 terms of the geometric sequence, substitute n = 1 through 5 into the equation.
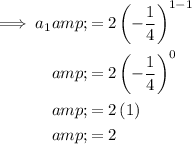
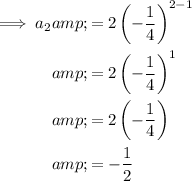
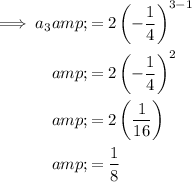
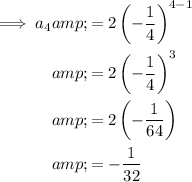
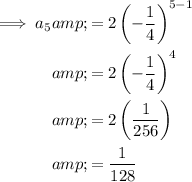
Therefore, the first 5 terms of the given geometric sequence are: