Answer:
Approximately
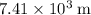 .
.
Step-by-step explanation:
If initial velocity, final velocity, and time taken are all found, then the change in height (displacement) can be found as:
![\begin{aligned}(\text{displacement}) &= \frac{(\text{average velocity})}{(\text{time taken})} \\ &= \frac{(1/2)[(\text{initial velocity}) + (\text{final velocity})]}{(\text{time taken})}\end{aligned}](https://img.qammunity.org/2023/formulas/physics/high-school/l51sjms5p74fpk5y88xizoj1lfh50jtkxa.png) .
.
For example, during the
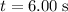 of constant acceleration at
of constant acceleration at
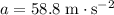 , initial velocity was
, initial velocity was
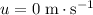 and final velocity would be:
and final velocity would be:
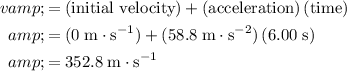 .
.
Displacement during this period of time would be:
![\begin{aligned}(\text{displacement}) &= \frac{(\text{average velocity})}{(\text{time taken})} \\ &= \frac{(1/2)[(\text{initial velocity}) + (\text{final velocity})]}{(\text{time taken})} \\ &= \frac{(1/2)\, (0\; {\rm m\cdot s^(-1)} + 352.8\; {\rm m\cdot s^(-1)})}{(6.00\; {\rm m\cdot s^(-1)})} \\ &\approx 1.058* 10^(3)\; {\rm m}\end{aligned}](https://img.qammunity.org/2023/formulas/physics/high-school/jjkvigler4akrkugri0hx9fstcnkpczqgq.png) .
.
During the next part of the flight, initial velocity was
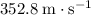 (from the first part of flight) and final velocity would be
(from the first part of flight) and final velocity would be
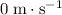 when the rocket reaches maximum height. Acceleration was given to be
when the rocket reaches maximum height. Acceleration was given to be
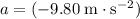 (negative since the rocket is accelerating downward,) but time is not known. Apply the following equation to find the change in height (displacement):
(negative since the rocket is accelerating downward,) but time is not known. Apply the following equation to find the change in height (displacement):
![\begin{aligned}(\text{displacement}) &= \frac{[(\text{final velocity})^(2) - (\text{initial velocity})^(2)]}{2\, (\text{acceleration})} \\ &\approx \frac{(0\; {\rm m\cdot s^(-1)})^(2) - (352.8\; {\rm m\cdot s^(-1)})^(2)}{2\, (-9.80\; {\rm m\cdot s^(-2)})} \\ &\approx 6.350* 10^(3)\; {\rm m}\end{aligned}](https://img.qammunity.org/2023/formulas/physics/high-school/vbg2dwkerk2emqy39x21tdoxnkr7sjvb88.png) .
.
The total change in height would be approximately
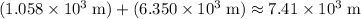 .
.