Question

NO LINKS!! Determine whether the sequence is geometric.

2, 4/√(3) , 8/3, 16/3√(3) , . . .

Choose:
1. Yes, the sequence is geometric
2. No, the sequence is not geometric

If so, find the common ratio. (if the sequence is not geometric, enter NONE)

Answer 1

Yes, the sequence is geometric.

`\textsf{Common ratio}=(2√(3))/(3)`

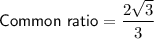
Explanation:

Given sequence:

`2, \; (4)/(√(3)),\; (8)/(3),\;(16)/(3√(3)),\;...`

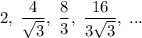
A geometric sequence has a common ratio.

Therefore, to check if the given sequence has a common ratio, divide each term by the previous term:

`\boxed{\begin{aligned}(16)/(3√(3)) / (8)/(3)&=(16)/(3√(3)) * (3)/(8)\\\\&=(48)/(24√(3))\\\\&=(2)/(√(3))\\\\&=(2√(3))/(3)\end{aligned}}`

`\boxed{\begin{aligned}(8)/(3) / (4)/(√(3))&=(8)/(3) * (√(3))/(4)\\\\&=(8√(3))/(12)\\\\&=(2√(3))/(3)\end{aligned}}`

`\boxed{\begin{aligned} (4)/(√(3)) / 2&= (4)/(√(3)) * (1)/(2)\\\\&= (4)/(2√(3)) \\\\&=(2)/(√(3))\\\\&=(2√(3))/(3)\end{aligned}}`

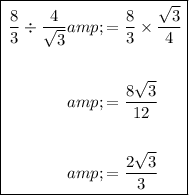
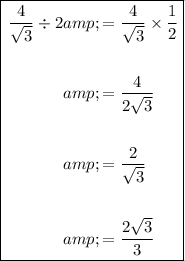
As there is a common ratio, the sequence is geometric.

The common ratio is:

• 
  `(2√(3))/(3)`

Answer 2

Geometric sequence has a common ratio.

Let's verify is the ratio of subsequent terms is common:

• 
  `r=t_2/t_1=(4/√(3))/2 = 2/√(3) =2√(3)/3`
• 
  `r=t_3/t_2=(8/3)/(4/√(3)) = 2/√(3) =2√(3)/3`
• 
  `r=t_4/t_3=(16/3√(3))/ (8/3) = 2/√(3) =2√(3)/3`

As wee se the ratio is common, it confirms that the sequence is geometric.

Common ratio is:

• 
  `r=2√(3)/3`