Question

a wooden block of mass 1200g, which moves on a horizontal surface, is subjected to a frictional force of 3 N. How much frictional force will act on the block if we put a 500g weight on it?​

Answer 1

Approximately
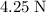`4.25\; {\rm N}` as long as the wooden block continues moving.

Step-by-step explanation:

Since the wooden block is moving, the friction on the block will be kinetic friction. This friction will be proportional to the magnitude of the normal force on the block. Specifically:

`\begin{aligned}& (\text{kinetic friction}) \\ =\; & (\text{normal force})\, (\text{kinetic friction coefficient $\mu_(k)$}) \end{aligned}`.

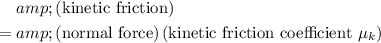In this question, since the surface is horizontal, the only vertical forces on this block will be:

• Weight of the block
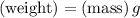  `(\text{weight}) = (\text{mass})\, g` where
  `g` is the gravitational field strength, and
• Normal force on the block.

These two forces will balance each other. Thus,
`(\text{normal force}) = (\text{weight})`.

`\begin{aligned}(\text{normal force}) &= (\text{weight}) \\ &= (\text{mass})\, g\end{aligned}`.

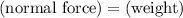Substitute to obtain:

`\begin{aligned}& (\text{kinetic friction}) \\ =\; & (\text{normal force})\, (\text{kinetic friction coefficient $\mu_(k)$}) \\ =\; & (\text{mass})\, (\text{kinetic friction coefficient $\mu_(k)$})\, g\end{aligned}`.

In other words, the kinetic friction on the block is proportional to the mass. As long as the block continues moving, increasing mass from
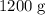`1200\; {\rm g}` to
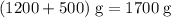`(1200 + 500)\; {\rm g} = 1700\; {\rm g}` will increase friction to
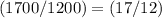`(1700 / 1200) = (17/12)` the initial value,
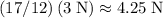`(17/12)\, (3\; {\rm N}) \approx 4.25\; {\rm N}`.