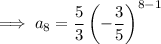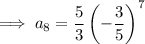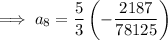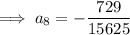Answer:
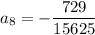
Explanation:

Given geometric sequence:
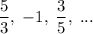
To find the common ratio, divide a term by the previous term:
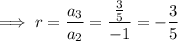
Substitute the found common ratio and given first term into the formula to create an equation for the nth term:
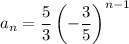
To find the 8th term, substitute n = 8 into the equation: