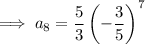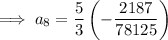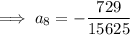Question

NO LINKS!! Find the specified term of the geometric sequence

a8: 5/3, -1, 3/5, . . .

a8=

Answer 1

`a_8=-(729)/(15625)`

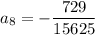
Explanation:

`\boxed{\begin{minipage}{5.5 cm}\underline{Geometric sequence}\\\\$a_n=ar^(n-1)$\\\\where:\\\phantom{ww}$\bullet$ $a$ is the first term. \\\phantom{ww}$\bullet$ $r$ is the common ratio.\\\phantom{ww}$\bullet$ $a_n$ is the $n$th term.\\\phantom{ww}$\bullet$ $n$ is the position of the term.\\\end{minipage}}`

Given geometric sequence:

`(5)/(3),\;-1,\;(3)/(5),\;...`

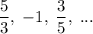
To find the common ratio, divide a term by the previous term:

`\implies r=(a_3)/(a_2)=((3)/(5))/(-1)=-(3)/(5)`

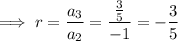
Substitute the found common ratio and given first term into the formula to create an equation for the nth term:

`a_n=(5)/(3)\left(-(3)/(5)\right)^(n-1)`

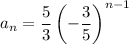
To find the 8th term, substitute n = 8 into the equation:

`\implies a_8=(5)/(3)\left(-(3)/(5)\right)^(8-1)`

`\implies a_8=(5)/(3)\left(-(3)/(5)\right)^(7)`

`\implies a_8=(5)/(3)\left(-(2187)/(78125)\right)`

`\implies a_8=-(729)/(15625)`