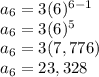Question

NO LINKS!! Find the specified term of the geometric sequence.

a6: a1 = 3, a2= 18, a3= 108, . . .

a6=

Answer 1

`a_(6) = 23,328`

Explanation:

⭐ Geometric Progression formula:
`a_(n) = a_1(b)^(n-1)`

• 
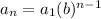
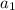  `a_(1)` is the first term of the geometric progression
• 
  `b` is the common ratio (the number each term gets multiplied by)
• 
  `a_(n)` is the notation for which term you are finding, where n is the term number

We are given that
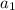`a_(1)` = 3. Now, we need to find b.

b is the quotient of
`(a__3)/(a__2)`.

• 
  `(a_3)/(a_2)\\ \\(108)/(18)\\= 6`
• 
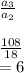
  `b` = 6

Let's substitute the first term and common ratio into the formula.

`a_n = 3(6)^(n-1)`

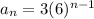
The problem wants us to solve for the 6th term, so we have to substitute 6 for n and solve.

`a_6 = 3(6)^(6-1)\\a_6 = 3(6)^5\\a_6 = 3(7,776)\\a_6 = 23,328`

Answer 2

23328

Explanation:

since it is a geometrics sequence we will use the formula

`{ar}^(n - 1)`

The first term(a) = 3

The second term = ar = 18

divide the first term and second term to find the common ratio

`(t2)/(t1) = (ar)/(a) = (18)/(3)`

r = 6

Now lets find the sixth term

`t6 = {ar}^(6 - 1)`

`t6 = {ar}^(5)`

by substituting for the values

`t6 = 3 * {6}^(5)`

= 3 × 7776

= 23328

i hope this helped