Question

I need some help understanding these questions, is there anyone willing to help? I'd really appreciate it!

Consider how the structure of the standard form of a linear function
reveals its key characteristics.

For the equation Ax + By = C , determine the slope, x -intercept,
and y -intercept.

Which form of a linear equation is more efficient for determining each characteristic?
- Slope
- x -intercept
- y -intercept

Answer 1

• Slope: slope-intercept form, point-slope form, or slope form
• X-intercept: intercept form, standard form
• Y-intercept: slope-intercept form, intercept form

Explanation:

You want to know how the form of a linear equation can be used to reveal its key characteristics.

Key Characteristics

The characteristics of a linear equation that are of interest for this problem are ...

• slope
• x-intercept
• y-intercept

Forms of a linear equation

A linear equation can be written in many forms. Some of these forms make it easy to determine one or more of the key characteristic listed above. Some of the more common forms are Slope-Intercept form, Point-Slope form, and Standard form. There are a number of others.

Slope-Intercept form

The slope-intercept form is ...

y = mx + b

where m is the slope, and b is the y-intercept. This form makes it easy to determine ...

• slope
• y-intercept

This equation cannot be used to describe a vertical line.

Alternate Slope-Intercept form

We can rearrange the above equation to reveal the x-intercept.

y = m(x -a)

where m is the slope and 'a' is the x-intercept. This form makes it easy to determine ...

• slope
• x-intercept

This equation cannot be used to describe a horizontal line (except y=0).

Point-Slope form

The equation of a line with slope m through point (h, k) can be written as ...

y -k = m(x -h)

This makes it easy to determine ...

• slope
• a point on the line (not necessarily an intercept)

This equation cannot be used to describe a vertical line.

Standard form

The standard form equation of a line is similar in style to the standard form equations for other geometric figures (circle, ellipse, hyperbola). This form is ...

Ax +By = C

where A, B, C are mutually prime (integers), and A ≥ 0. If A = 0, then B > 0. That is, the leading coefficient is positive. Integers are preferred for the coefficients, but some lines have irrational slope or other key characteristics, so integers may not be able to be used in all places.

The key characteristics cannot be read from the equation directly, but they are one step away:

• slope = -A/B
• x-intercept = C/A
• y-intercept = C/B

Solving for the intercepts is especially easy, so we list this form as one that can be efficient for determining the intercepts.

Intercept form

A very nice form for efficiently determining the intercepts, or efficiently writing an equation from the intercepts is ...

x/a +y/b = 1

where 'a' is the x-intercept, and 'b' is the y-intercept. This form makes it very easy to determine ...

• x-intercept
• y-intercept

You may notice that dividing the standard form equation by C and rearranging the coefficients will give you this form:

Ax +By = C

(A/C)x +(B/C)y = 1 . . . . . . . divide by C

x/(C/A) +y/(C/B) = 1 . . . . . . . intercept form

General form

The general form of a polynomial equation of any degree is ...

f(x, y) = 0

The general form of a linear equation is ...

Ax +By +C = 0

This is simply a rearrangement of the Standard form equation. Equations written in this form can be helpful for ...

• finding the distance from a point to the line
• solving a system of equations by "addition" or matrix methods

Various 2-Point forms

When two points are given, and you want an equation of the line, various forms are available for using those coordinates. These forms make use of the fact that the slope of a line is the same everywhere, so the ratio of any difference of y-coordinates to the corresponding difference of x-coordinates is a constant (the slope). Again, slopes of 0 or "undefined" can cause trouble with certain of these forms. Here are several different arrangements of 2-point forms:

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)\\\\(x_2-x_1)(y-y_1)=(y_2-y_1)(x-x_1)\\\\(y-y_1)/(x-x_1)=(y_2-y_1)/(x_2-x_1)=m\qquad\text{Slope form}\\\\\\(x-x_1)/(y-y_1)=(x_2-x_1)/(y_2-y_1)\qquad\text{inverted from the above}\\\\\\(y-y_1)/(y_2-y_1)=(x-x_1)/(x_2-x_1)`

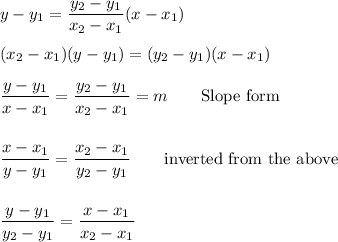
The last three "ratio forms" are variations of each other. Any such proportion can be written 4 ways. (3 are shown) The form not shown has the variables in the denominator, which is usually not useful.

All of these forms can be written in a "general form" by subtracting one side.

The slope can be read directly from the 1st and 3rd of the forms shown here. It is m = (y2-y1)/(x2-x1).

The slope form is useful for determining ...

• slope

Determinant form

Another 2-point form is one written as a determinant:

`\left|\begin{array}{cc}x-x_1&x_2-x_1\\y-y_1&y_2-y_1\end{array}\right|=0`

__

Additional comment

It can be useful to recognize the various forms and their relationship to known points on the line or other key characteristics of the function. Any of the slope or point-slope forms make it easy to write the equations of parallel or perpendicular lines through a given point. (The standard and general forms can be used for this, too.)