Given:



To find:


Solution:-

Ad we know Area of rhombus has two Formulas:-

First :-
Area = (Diagonal 1 × Diagonal 2)/2

Second:-
Area = B × h

As we know in this case base and height aren't given, so we will use first formula to find rhombus.

We know:-

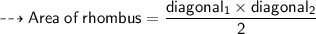







know more :-

