Question

How many different 9-letter strings can be made by rearranging the characters in the word WISCONSIN?

a. 9^6
b. 9! / 8
c. C(9,6)
d. 9!
e. 9! / 6

Answer 1

d. 9!

To solve this problem, you can use the permutation formula, which is given by the following:

`$$P_(n)^(r) = (n!)/((n - r)!)$$`

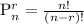
In this formula,
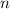`$n$` is the total number of items, and
`$r$` is the number of items being chosen at a time.

In this case, we have a total of 9 letters in the word WISCONSIN, and we want to rearrange them to form 9-letter strings. Therefore, we can use the permutation formula as follows:

`$$P_(9)^(9) = (9!)/((9 - 9)!) = (9!)/(0!) = 9! = \boxed{362,!880}$$`

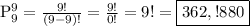
This means that there are 362,880 different 9-letter strings that can be made by rearranging the characters in the word WISCONSIN.