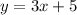Question

What is the slope-intercept form of a line that passes through points (2, 11) and (4, 17)?y = negative 3 x minus 5y = 3 x minus 5y = negative 3 x + 5y = 3 x + 5.

Answer 1

y = 3x + 5

Explanation:

The slope-intercept form of a line is
`y = mx + b`, where m is the slope, and b is the y-intercept.

To solve for m (the slope), use the formula:
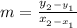`m = (y__(2) - y__(1))/(x__(2) - x__(1))`, where
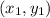`(x_(1) , y_(1) )` and
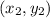`(x_(2), y_(2))` are the points you are given.

. . . . . . . . m = (17 - 11) / (4-2)

. . . . . . . . m = 6/2

. . . . . . . ∴ m = 3

Substitute the slope, m, into the slope-intercept equation.

y = 3x + b

Now we have to solve for b, the y-intercept. To do so, substitute a point that was given to you into the equation.

I chose the point (4,17), but you can also do (2,11).

. . . . . . . . 17 = 3(4) + b

. . . . . . . . . . remember that the x-variable is being multiplied to the m

. . . . . . . . -12 + 17 = 12 + b - 12

. . . . . . . . ∴ 5 = b

Substitute the y-intercept, b, into the slope-intercept equation, and you're done!

`y = 3x + 5`