Answer:
P/Q = (-3x +2)/(3(3x -1))
PQ = 12/((3x -1)(-3x +2))
Explanation:
You want the quotient and product of P(x) = 2/(3x -1) and Q(x) = 6/(-3x +2).
Quotient
The quotient is found by multiplying by the inverse of the denominator:
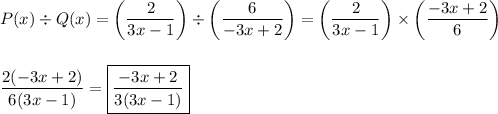
Product
As with multiplying any fractions, the numerator is the product of the numerators, and the denominator is the product of the denominators.
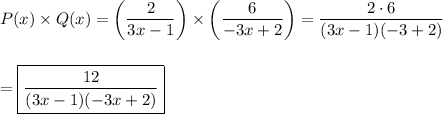
__
Additional comment
Usually the simplified form would contain no parentheses. The indicated products would be multiplied out.