Answer:
B. x=2 and D. x=-10
Explanation:
We have the quadratic formula:
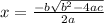
Quadratic equations are in the form

We have to get the equation equal to zero before we can use the quadratic formula so subtract 20 from both sides and we get

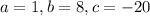
Now we plug these values into the quadratic equation
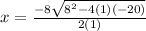
Now we solve for x
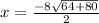
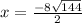
Now we get two equations because the square root gives us both a positive and a negative answer.
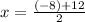 and
and

Let's solve the first one now


Now the second one
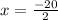
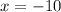
so
 and
and
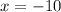
so the answers are B and D.
Hope this helps!