Question

At the circus, a 100. -kilogram clown is fired at 15 meters per second from a 500. -kilogram cannon. What is the recoil speed of the cannon?.

Answer 1

`3.0\; {\rm m\cdot s^(-1)}`.

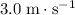Step-by-step explanation:

When an object of mass
`m` travels at a velocity of
`v`, the momentum
`p` of that object will be
`p = m\, v`.

Assume that the clown and the cannon were both initially at rest (
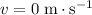`v = 0\; {\rm m\cdot s^(-1)}`.) The initial momentum of both the clown and the cannon will be
`0\; {\rm kg \cdot m\cdot s^(-1)}`:

`\begin{aligned}& (\text{initial clown momentum}) \\ =\; & (\text{mass of clown}) \, (\text{initial clown velocity}) \\ =\; & (100\; {\rm kg}) \, (0\; {\rm m\cdot s^(-1)}) \\ =\; & 0\; {\rm kg\cdot m\cdot s^(-1)}\end{aligned}`.

`\begin{aligned}& (\text{initial cannon momentum}) \\ =\; & (\text{mass of cannon}) \, (\text{initial cannon velocity}) \\ =\; & (500\; {\rm kg}) \, (0\; {\rm m\cdot s^(-1)}) \\ =\; & 0\; {\rm kg\cdot m\cdot s^(-1)}\end{aligned}`.

It is given that immediately after launch, the velocity of the clown was
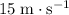`15\; {\rm m\cdot s^(-1)}`. The momentum of the clown would be:

`\begin{aligned}& (\text{clown momentum after launch}) \\ =\; & (\text{mass of clown}) \, (\text{clown velocity after launch}) \\ =\; & (100\; {\rm kg}) \, (15\; {\rm m\cdot s^(-1)}) \\ =\; & 1500\; {\rm kg\cdot m\cdot s^(-1)}\end{aligned}`.

While the velocity of the cannon right after launch is unknown, note that this value can be found from the momentum of the cannon right after launch:

`p = m\, v`.

`\begin{aligned}v &= (p)/(m)\end{aligned}`.

`\begin{aligned}& (\text{cannon recoil velocity}) = \frac{(\text{cannon recoil momentum})}{(\text{cannon mass})}\end{aligned}`.

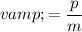The momentum of the cannon right after launching can be found using the conservation of momentum. Specifically, the momentum of the clown and the cannon will be the same ("conserved") right before and after the launch:

`\begin{aligned}& (\text{initial clown momentum}) + (\text{initial cannon momentum}) \\ &= \\ & (\text{clown momentum after launch}) + (\text{cannon recoil momentum})\end{aligned}`.

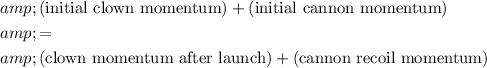Thus:

`\begin{aligned}& (0\; {\rm kg \cdot m\cdot s^(-1)}) + (0\; {\rm kg \cdot m\cdot s^(-1)}) \\ &= \\ & (1500\; {\rm kg \cdot m\cdot s^(-1)}) + (\text{cannon recoil momentum})\end{aligned}`.

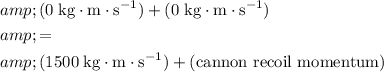Rearrange to obtain the cannon momentum right after launch (recoil momentum):

`\begin{aligned}(\text{cannon recoil momentum}) = (-1500)\; {\rm kg\cdot m\cdot s^(-1)}\end{aligned}`.

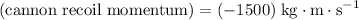(Negative since the cannon is moving backwards, away from the clown.)

Therefore, the recoil velocity of the cannon would be:

`\begin{aligned}& (\text{cannon recoil velocity}) \\ =\; & \frac{(\text{cannon recoil momentum})}{(\text{cannon mass})} \\ =\; &\frac{(-1500)\; {\rm kg \cdot m\cdot s^(-1)}}{500\; {\rm kg}} \\ =\; & (-3)\; {\rm m\cdot s^(-1)}\end{aligned}`.

The recoil speed of the cannon will be
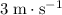`3\; {\rm m\cdot s^(-1)}`.