Question

How do you solve a system of linear equations using substitution or elimination?

Answer 1

Refer to the step-by-step explanation. If you need any clarification on a part just add a comment under this answer :)

Explanation:

Given a system of equations, there are a few methods to calculate solutions of that system. Two ways to do so are by using elimination or substitution.

To solve a set of equations by elimination you will take two equations and either add or subtract them to eliminate one of the variables. Here is a quick example...

`\left \{ {{3x+y=5} \atop {2x-y=0}} \right.`

If we were to add these equations together, we could eliminate the variable
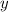`y\\` to get an equation to solve for
`x`.

After adding these equations we get:
`5x=5`

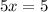
We then can solve the equation for
`x\\`, to find the value of
`x`, and use that value to plug back (a.k.a substitute) into the other equations to solve for
`y`

To solve a set of equations by substitution you will take a system of equations, pick one of the equations and solve one of them for one variable. Here is a quick example...

`\left \{ {{3x+2y=16} \atop {7x+y=19}} \right.`

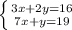
If we take the second equation and solve for the variable,
`y`, we will get an equation in terms of
`x`. We can then take that equation and plug it into the top, substituting
`y`, for the equation in terms of
`x`. Like so....

Solving bottom equation for
`y`, we get:
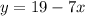`y=19-7x`, now substitute this equation for
`y` into the top equation.

We get:
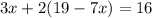`3x+2(19-7x)=16`, you now have an equation only in terms of
`x`, so you can solve for
`x`. I won't complete the whole problem but hopefully you get the idea :)