Question

NO LINKS!! Please help me with this statement Part 7 ll​

Answer 1

(a) t = 2, N = 204

t = 14, N = 603

t = 24, N = 786

(b) 1500 deer

Explanation:

Given function:

`N=(20(5+3t))/(1+0.04t), \quad t \geq 0`

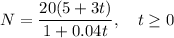
Part (a)

`\boxed{\begin{aligned}t = 2 \implies N&=(20(5+3(2)))/(1+0.04(2))\\\\&=(20(5+6))/(1+0.08)\\\\&=(20(11))/(1.08)\\\\&=(220)/(1.08)\\\\&=203.703703...\\\\&=204\end{aligned}}`

`\boxed{\begin{aligned}t = 14 \implies N&=(20(5+3(14)))/(1+0.04(14))\\\\&=(20(5+42))/(1+0.56)\\\\&=(20(47))/(1.56)\\\\&=(940)/(1.56)\\\\&=602.56410...\\\\&=603\end{aligned}}`

`\boxed{\begin{aligned}t = 24 \implies N&=(20(5+3(24)))/(1+0.04(24))\\\\&=(20(5+72))/(1+0.96)\\\\&=(20(77))/(1.96)\\\\&=(1540)/(1.96)\\\\&=785.71428...\\\\&=786\end{aligned}}`

Part (b)

To find the limiting size of the herd, find the horizontal asymptote of the function.

As the degree of the numerator is equal to the degree of the denominator, the asymptote is the result of dividing the highest degree term of the numerator by the highest degree term of the denominator.

Expand the numerator of the function:

`N=(20(5+3t))/(1+0.04t)=(100+60t)/(1+0.04t)`

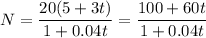
Divide 60t by 0.04t:

`\textsf{Horizontal asymptote}:\;y=(60t)/(0.04t)=1500`

Therefore, the limiting size of the herd as time increases is 1500.